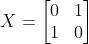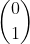Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.

Introduction

This tutorial will introduce you to unitary matrices and how they are used for representing quantum logic gates.

Qubits and vectors

For qubits the computational basis (0 and 1) is represented by two ket vectors:

|0⟩ = 0

|1⟩ = 1

These vectors can be represented as column vectors which are very useful as you will find later:

|1〉=

|0〉=

Matrices are very powerful in quantum computing as they can be used to represent quantum logic gates.

For example the Pauli-X gate:

This is a single qubit gate that flips |0⟩ to |1⟩ and vice versa.

In matrix form it is represented as:

Using this matrix we can use matrix multiplication to see how the Pauli-X gate operates on an input state.

For example if our input state is |1〉:

|1〉=

We then multiply the column vector corresponding to |1〉by the Pauli-X matrix:

Which = |0〉which is correct as the X gate flips |1〉to |0〉and vice versa.

Likewise if our input state is |0〉:

|0〉=

Then again multiply the Pauli-X matrix by the column vector corresponding to |0〉:

Which = |1〉

The Z-gate is a single qubit gate that flips the phase of the qubit such that |0〉is unchanged but |1〉is flipped to -|1〉

We have released a separate tutorial on the Z-gate in detail: https://quantumcomputinguk.org/tutorials/z-gate

The identity matrix for the Z-gate is :

Let’s see how the Z matrix transforms the state of |1〉:

Remember that the column vector for |1〉:

We then multiply the column vector by the Z matrix:

Which = -|1〉