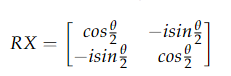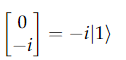Introduction to the RX gate with code

Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.

Introduction

In this tutorial we will explore the RX gate how to implement it in Qiskit.

The RX gate is a gate that does a rotation around the X-axis by a specified angle which is normally denoted by θ.

The matrix for the RX gate is:

Using matrix multiplication we can see how the RX gate operates on the qubits state. For our first example lets initialise the qubits state to |0〉 and set θ to be π. Then we multiply the associated column vector for |0〉with the RX matrix. This should flip the qubits state from |0〉to −i|1〉

The associated column vector for |0〉is:

Then multiply the column vector by the RX matrix:

If we instead initialise the qubit to |1〉:

This has transformed the state from |1〉to −i|0〉

Implementation

In Qiskit we can implement an RX gate very easily using the following function:

circuit.rx(pi,q[0])

Where pi is the rotation amount and q[0] is the qubit we want to apply the RX gate to.

Go to the code section for the full code example.

How to run the program

Copy and paste the code below in to a python file

1. Enter your API token in the IBMQ.enable_account('Insert API token here') part

2. Save and run

Code

from qiskit import QuantumRegister, ClassicalRegister
from qiskit import QuantumCircuit, execute,IBMQ
from qiskit.tools.monitor import job_monitor
import numpy as np

IBMQ.enable_account('ENTER API KEY HERE')
provider = IBMQ.get_provider(hub='ibm-q')

backend = provider.get_backend('ibmq_qasm_simulator')

pi = np.pi

q = QuantumRegister(1,'q')
c = ClassicalRegister(1,'c')

circuit = QuantumCircuit(q,c)

circuit.rx(pi,q[0])
circuit.measure(q,c)

print(circuit)

job = execute(circuit, backend, shots=8192)

job_monitor(job)
counts = job.result().get_counts()

print(counts)

Output