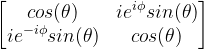Introduction

Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.

This tutorial is the second tutorial in the series on Photonic Quantum Computing with the Perceval API from Quandela. In this tutorial we will look at how to implement a Z-gate a using a phase shifter.

If you missed the first tutorial on Photonic Quantum Computing with the Perceval then you can find it here:

https://quantumcomputinguk.org/tutorials/optical-quantum-computing-with-perceval

What is a phase shifter?

A phase shifter is an optical component that adds a phase (denoted as ϕ) on a spatial mode. This corresponds to a rotation on the Z-axis of the Bloch sphere. As such we can implement a Z-gate by rotating the phase by π radians.

Implementation

In order to show how the phase shifter will affect the qubits state we will be implementing the photonic circuit above. This consist of two beam splitters and a phase shifter which will implement the Z-gate on mode 2.

To see how the circuit affects the qubits state we will go through it step

Step 1: Apply the first beam splitter

The first step is to put the qubit in to superposition using a beam splitter. The beam splitter is represented using the following unitary matrix:

For the beam splitters parameters we set the reflectivity (ϴ) to π/4 and the phase (ϕ) to π. If the qubits state is initialised to |0〉then beam splitter will affect the qubits state like so:

Which has put the qubit in to superposition much like a Hadamard gate!

Step 2: Apply a Z-gate using a phase shifter

The second step is to apply the Z-gate using a phase shifter. This is a component that is applied to only 1 mode and can be described using the following unitary matrix:

To implement a Z-gate we will need to set ϕ to π as the Z-gate rotates the phase of the qubit by π radians.

The phase shifter will affect the qubits state like so:

Which has flipped the phase of mode 2.

Step 3: Apply the second beam splitter

The last step is now to apply a second beam splitter to bring the qubit out of superposition. The final qubit state will be |1〉instead of |0〉due to the phase flip from the Z-gate.

Code

import perceval as pcvl
import perceval.lib.phys as phys
import sympy as sp


circuit = phys.Circuit(2)
circuit.add((0, 1), phys.BS(theta=sp.pi/4, phi_b=0)) # Beam Splitter
circuit.add((0),phys.PS(sp.pi)) # Z-gate using phase shifter
circuit.add((0, 1), phys.BS(theta=sp.pi/4, phi_b=0)) # Beam Splitter

simulator_backend = pcvl.BackendFactory().get_backend("Naive")
simulator = simulator_backend(circuit.U)

pcvl.pdisplay(circuit)
ca = pcvl.CircuitAnalyser(simulator,[pcvl.BasicState([0, 1]), pcvl.BasicState([1, 0])])

pcvl.pdisplay(ca)

Photonic Quantum Computing with Perceval: Z-gate using a phase shifter