How to implement quantum computing in software development

Interested in learning how to program quantum computers? Then check out our Qiskit textbook Introduction to Quantum Computing with Qiskit.

Introduction

This guide will provide the basic steps needed to successfully implement quantum computing in to a software application that you are developing.

Step 1: Work out if your application requires quantum computing 

Despite quantum computing often being touted as the next big revolution in computing there are many problems where a classical computer can actually outperform a quantum computer. One good example is basic arithmetic. A computer can do arithmetic on the order of nanoseconds due to the fact that they have dedicated logic in the form of ALUs. Quantum computers however have no such dedicated hardware and are quite slow in comparison. Their power does not lay in speed but in the fact that they can make use of quantum parallelisation.  

In fact on specific quantum devices called annealing processors it is often better for the runtime to be as slow as possible since if the runtime is too fast the solution will be nonoptimal.

What types of problems can Quantum Computers solve?

Quantum computers tend to be able to solve problems that have a very high search space. For example, consider a database. Let's say you need to search a database for an entry. The worst case scenario for a classical computer is that it will have to go through the entire database to find the entry you wish to find. This corresponds to a computational complexity of O(N). 

However with quantum computing it is possible to solve such problems more efficiently and with less computational complexity. For example a quantum algorithm called Grover’s search algorithm can solve the problem in O(√N) time. 

See our Qiskit tutorial on Grover’s algorithm here: https://quantumcomputinguk.org/tutorials/grovers-algorithm-with-code

Step 2: Find the right quantum device 

Now that we have worked out our application can benefit from quantum computing we now need to find the right device. The field of quantum computing is a burgeoning one and as such there have been many different advancements. As a result there have been many different quantum devices developed each with their own pros and cons. As such when developing an application it is important to know which device is best depending on the problem you wish to solve. 

Gate based Quantum Computing

The most popular type of quantum device is the gate based quantum computer. This is a quantum computer where operations are done on qubits using quantum logic gates. These logic gates are much like the logic gates found in classical computers but are more complex. 

Here are some examples: 

• Hadamard Gate: This logic gate puts a qubit in to a superposition of states and is arguably the most important quantum logic gate 

• Pauli gates: These are a set of gates that rotate the qubits state by 180 degrees on different axes. A X-gate rotates the state around the X axis while the Z-gate rotates around the Z axis. There’s also a Y-gate that rotates around the Y axis

• Controlled NOT (CNOT): This is a multi qubit gate that operates on a qubit based upon the state of another. If the control qubit is 1 then the target qubits state will be flipped from 0 to 1 or vice versa

Gate based quantum computers are general purpose and such can be used for any problem that requires quantum parallelisation. For example factoring numbers using Shor’s algorithm or efficient search using Grover’s search algorithm. Machine learning can also be done using variational quantum circuits. 

There are many different hardware implementations of gate based quantum computing:

1. Superconducting quantum devices: The most popular hardware implementation that use noisy quantum circuits with a qubit count ranging between 5 and 53 qubits. They also tend to have to be cooled using refrigeration.

2. Trapped ion devices: These use trapped ions as qubits. These devices tend to have very high fidelity qubits with much higher coherence times but a lower qubit count compared to superconducting devices.

3. Photon based devices: These use photons as qubits. These devices tend to have a high fidelity and fast gate operations and do not require refrigeration.

The best way to get in to gate based quantum computing is through the IBM Quantum Experience as IBM have made their superconducting devices open access: https://quantum-computing.ibm.com/

To start programming gate based quantum devices the easiest way is to use Qiskit and Python. Qiskit is a library that allows you to create quantum circuits and run them on IBM’s quantum devices: https://qiskit.org/

Quantum Annealers

This type of quantum computer is designed specifically for solving optimisation problems. For example the Travelling Salesman problem which corresponds to finding the most optimal route around a city. On quantum annealers this is done by first initializing the qubits into superposition. After this the qubits and connections between them are slowly tuned such that at the end of runtime the configuration corresponds to the optimal solution of interest. 

The easiest way to get in to quantum annealing is through D-Wave as they have made their annealers open access:

https://cloud.dwavesys.com/leap/signup/

Picking a device based upon qubit/gate error

Another issue to look at when picking a quantum device is the issue relating to qubit and gate errors. For example superconducting quantum devices are very prone to noise which can lead to errors. These errors come in 3 types (bit flips, phase flips, and readout errors). These can be corrected using quantum error correction/mitigation methods however these may require additional qubits and gates in the quantum circuits. 

As such it is best to pick the best device based upon qubit error rates. For example one device may have low fidelity qubits that are prone to error while another may have very high fidelity qubits and as such a lower probability of errors occurring.

In qiskit qubit error rates for quantum devices can be found using the backend monitor:

See our tutorial here on how to get device information such as error rates in qiskit: https://quantumcomputinguk.org/tutorials/how-to-get-real-time-information-on-ibm-quantum-devices

Step 3: Create a quantum algorithm to solve the problem 

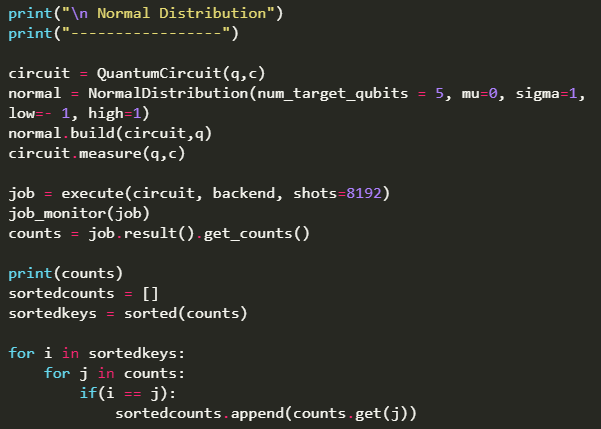
After you have picked the right device to solve the problem you will have to create a quantum algorithm. In gate based quantum computers this could be a small circuit. For example if you wanted to create a 32 qubit random number generator you would simply create a quantum circuit that initialises 32 qubits into superposition using Hadamard gates. Then you would measure the qubits and the results would be brought back into your application. 

Obviously depending on your problem your quantum circuit may be way more complex. Your algorithm may even be hybrid and contain a classical part of the algorithm and a quantum part consisting of a circuit. Some may be variational quantum circuits where the state of the qubit is measured then reupdated each time based upon the problem of interest.

In your algorithm you should be making use of either superpositoning or entanglement. These are quantum mechanical effects that allow quantum computers to outperform classical computers. If your algorithm does not make use of either of these then there is a good chance your algorithm will not outperform its classical equivalent.

In gate based quantum computing this is easy to check. If your circuit uses Hadamard gates then it is using superpositioning. If your circuit creates bell states with Hadamard gates and multi qubit gates then it is using entanglement.

Circuit diagram of a bell pair consisting of a Hadamard gate and a CNOT gate. This is one of the simplest forms of entanglement

See our tutorials on how to implement quantum algorithms in Qiskit: https://quantumcomputinguk.org/tutorials-1

Step 4: Test the performance of your quantum algorithm 

A common mistake among developers is to create a quantum algorithm that seems to work but does not have a quantum advantage. A quantum advantage can be defined as when a quantum computer can solve a problem much faster than a classical computer. If your quantum algorithm can be beaten by a classical equivalent then there is no point even using your algorithm. 

As such it is very important that you test your quantum algorithm against a classical one. If your algorithm has lower performance then use the classical algorithm instead. An application that has a speedup from QC is excellent but if there is no speedup then it is simply a gimmick.